目次
問題文
複数台のPCで1台のプリンターを共有するシステムがある。このプリンターに対する平均要求回数が毎分1回のとき,このプリンターの平均印刷時間(印刷を要求してから終了するまでの時間)は何秒か。ここで,プリンターは,平均が15秒の指数分布に従う時間で印刷要求を処理するものとし,プリンターに対する印刷要求はポアソン分布に従うものとする。
ア 15
イ 18
ウ 20
エ 30
解説
解答
ウ
この問題は 待ち行列理論(M/M/1モデル) をベースにした計算問題です。順を追って整理してみましょう。
与えられた条件
- 到着率 λ(プリンタへの平均要求回数):毎分 1 回
→ 1/60 秒⁻¹ = 0.0167 回/秒 - サービス時間の平均:15 秒
→ サービス率 μ = 1/15 = 0.0667 回/秒 - サービス時間は 指数分布 に従う → M/M/1 待ち行列モデルが適用可能
- 要求到着は ポアソン分布 に従う → M/M/1 の前提に一致
利用率の計算
利用率 ρ は
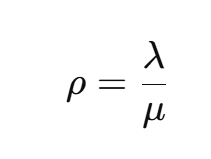
で求められます。
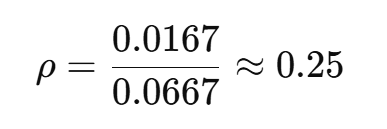
したがって、このプリンタは 25%の稼働率 です。
平均システム滞在時間(待ち時間+処理時間)
M/M/1 モデルにおける平均応答時間(滞在時間) W は次式で表されます。
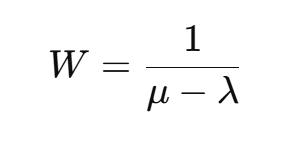
代入すると
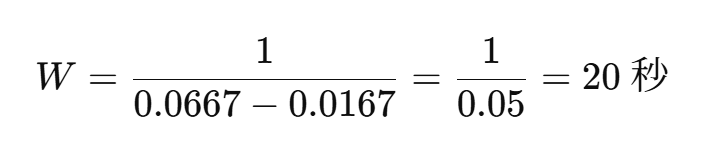
まとめ
- 待ち行列理論 M/M/1 を適用
- 利用率は 25%
- 平均滞在時間は 20 秒
したがって、正解は ウ:20 秒 です。


